leetcode_105. 从前序与中序遍历序列构造二叉树 & 106

2 minutes read
LeetCode
面试 • 算法 • 数据结构

105. 从前序与中序遍历序列构造二叉树

描述

根据一棵树的前序遍历与中序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树：

     3
    / \
    9 20
      / \
      15 7

https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal

思路

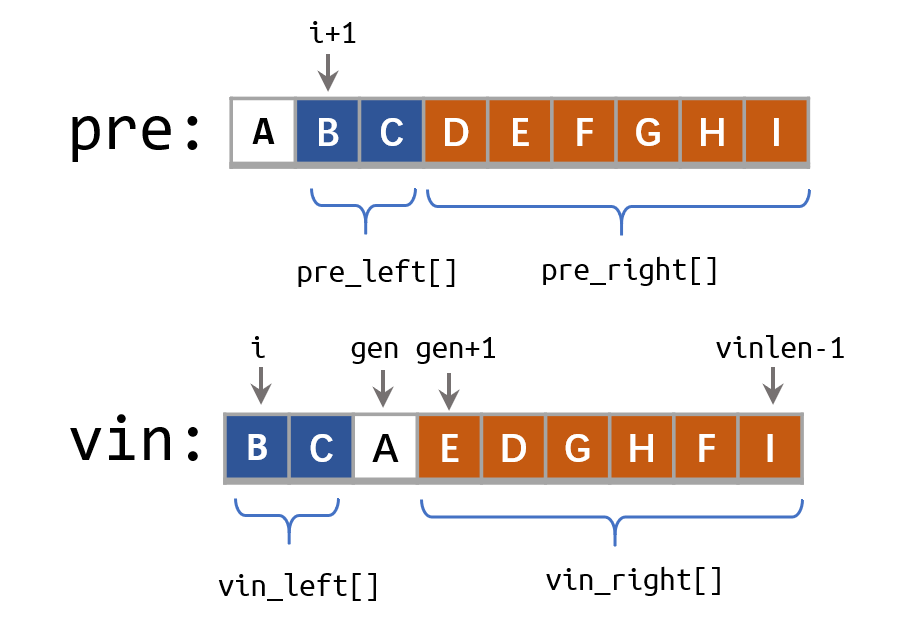
  1. 由先序序列第一个pre[0]在中序序列中找到根节点位置gen
  2. 以gen为中心遍历
    • 0~gen左子树
      • 子中序序列：0~gen-1，放入vin_left[]
      • 子先序序列：1~gen放入pre_left[]，+1可以看图，因为头部有根节点
    • gen+1~vinlen为右子树
      • 子中序序列：gen+1 ~ vinlen-1**放入vin_right[]
      • 子先序序列：gen+1 ~ vinlen-1**放入pre_right[]
  3. 由先序序列pre[0]创建根节点
  4. 连接左子树，按照左子树子序列递归（pre_left[]和vin_left[]）
  5. 连接右子树，按照右子树子序列递归（pre_right[]和vin_right[]）
  6. 返回根节点

1566200965090

1566200739629

解答

我在LeetCode上的解答

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(preorder []int, inorder []int) *TreeNode {
	if preorder == nil || inorder == nil ||
		len(preorder) == 0 || len(inorder) == 0 {
		return nil
	}

    // 中顺序列找根结点
    var root int
    for k, v :=  range inorder {
        if v == preorder[0] {
            root = k
            break
        }
    }

    // 左右子树归类
    // pre_left, pre_right := preorder[1: root+1], preorder[root+1:]
    // in_left, in_right := inorder[0: root], inorder[root+1:]
    
    // 左右子树递归
    return &TreeNode{
        Val:   preorder[0],
        Left:  buildTree(preorder[1: root+1], inorder[: root]),
        Right: buildTree(preorder[root+1:], inorder[root+1:]),
    }
}

结果和优化

执行用时 :4 ms, 在所有 Go 提交中击败了95.95%的用户 内存消耗 :3.9 MB, 在所有 Go 提交中击败了68.15%的用户

原则：

  1. 能不创建变量就不创建
  2. 要用的时候再创建（因为可能提前退出）
  3. 语言本身能实现的优先交给语言来：line30，31 直接用切片不香吗，就没必要自己创建变量写循环了

106. 从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(inorder []int, postorder []int) *TreeNode {
    l := len(postorder)
    if l == 0 {
        return nil
    }

    // post:9, 15, 7, 20, 3
    // in:  9, 3, 15, 20, 7
    var k, v int
    for k, v = range inorder {
        if v == postorder[l-1] {
            break
        }
    }
    

    return &TreeNode{
        Val:   v,
        Left:  buildTree(inorder[:k], postorder[:k]),
        Right: buildTree(inorder[k+1:], postorder[k: l-1]),
    }

}

分享：